[線性系統] 離散時間系統的可觀察性質 (Observability)

考慮 離散時間 線性非時變 (Discrete Time Linear Time Invariant, DT-LTI)系統
$$\begin{array}{l} x(k + 1) = Ax(k)\\ y(k) = Cx(k) \end{array}$$ $x \in \mathbb{R}^n, y \in \mathbb{R}^p$。

我們說上述系統為 可觀察 (observable) 或稱 $(A,C)$ 可觀察 若下列條件成立：
存在 常數 $N < \infty$ ，使得對任意 初始狀態 $x(0)$ 而言，可用 $N$ 組量測輸出 $\{y(0), y(1),...,y(N-1)\}$  uniquely 決定該初始狀態 $x(0)$。

Comment
1. 上述定義可類比 可控制性條件，

2. 事實上若我們無法透過 $n$ 組 量測輸出 來區別 $x(0)$ 則就算給額外再多的量測輸出 e.g., $N>n$ 組 仍無法區別 $x(0)$。(此結果可由 Cayley-Hamilton Theorem 證明。)

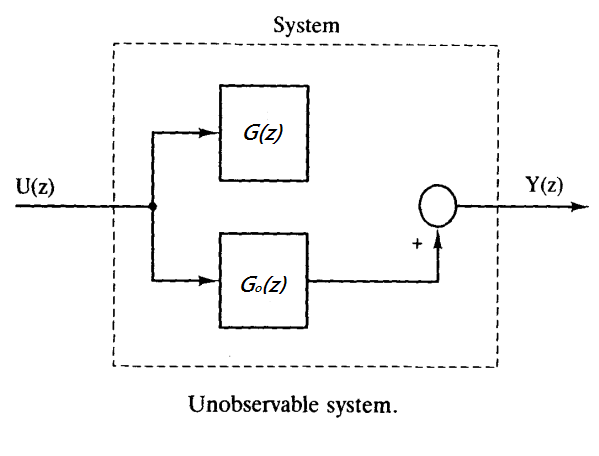
以下我們看個 unobservable 的例子

上方的方塊圖 顯示了 子系統 $G(z)$ 的狀態 無法從輸出 $Y(z)$ 觀察到。 (圖中的 $(z)$ 表示對原系統做 Z-transform。)

觀察性基本問題：
透過 sensor 所量測到的輸出 $y$ 是否足夠讓我們找出系統 初始狀態 $x(0)$ uniquely?

為何我們關心 初始狀態? 因為一但有初始狀態則其餘任意時刻狀態均可透過狀態方程求解獲得。亦即 給定 $x(0)$ 則
$$\left\{ \begin{array}{l} x(1) = Ax(0)\\ x(2) = {A^2}x(0)\\ ...\\ x\left( N \right) = {A^N}x\left( 0 \right) \end{array} \right.$$ 故若給定初始狀態 $x(0)$ 則其餘任意時刻狀態 $x(1), x(2),...,x(N)$均可透過狀態方程 $x(k+1) = Ax(k)$ 獲得。

但現在我們僅給定 $y(0),...,y(N)$ 亦即我們僅知道
$$\Rightarrow \left\{ \begin{array}{l} y(0) = Cx(0)\\ y(1) = Cx(1) = CAx(0)\\ y(2) = Cx(2) = C{A^2}x(0)\\ ...\\ y\left( N \right) = C{A^N}x\left( 0 \right) \end{array} \right.$$ 或者更進一步改寫成矩陣形式
$$\left[ {\begin{array}{*{20}{c}} {y(0)}\\ {y(1)}\\  \vdots \\ {y(N)} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} C\\ {CA}\\  \vdots \\ {C{A^N}} \end{array}} \right]x\left( 0 \right)$$ 想問是否可從這些 $\{y(0),...,y(N)\}$ 回推 $x(0)$ (uniquely!)。 如果可以我們稱系統可觀察，若不行我們稱系統不可觀察。

Comment:
回憶在線性代數中，我們說 $Ax = b$ 解存在 若且唯若 $A$ 有 indepenent row (此對應 controllabilility problem)；若我們說 $Ax = b$ 有唯一解 (注意 唯一不保證存在!!)，若且為若 $A$ 有 independent column (此對應 observability problem)。

故我們要求觀察性矩陣 $O$ ( 其維度 $\dim(O) = Np  \times n$)
$$O = \left[ {\begin{array}{*{20}{c}} C\\ {CA}\\  \vdots \\ {C{A^N}} \end{array}} \right]$$ 有 independent column。由 Caley-Hamilton Theorem ，我們可僅考慮 $n$ 個量測輸出，則我們有
$$\left[ {\begin{array}{*{20}{c}} {y(0)}\\ {y(1)}\\  \vdots \\ {y(n - 1)} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} C\\ {CA}\\  \vdots \\ {C{A^{n - 1}}} \end{array}} \right]x\left( 0 \right)$$ 故觀察性矩陣 $O$ ( 其維度 $\dim(O) = np  \times n$)
$$O = \left[ {\begin{array}{*{20}{c}} C\\ {CA}\\  \vdots \\ {C{A^{n - 1}}} \end{array}} \right]$$ 需要有 full column rank $n$ 我們總結 可觀察性的測試如下：

Theorem: Observability Rank Test
若系統 $(A,C)$ 為 observable 若且唯若 $rank(O) = n$。

同樣的我們也有 Hautus Lemma for observability

Lemma: Hautus Lemma for observability
一個系統為 observable 若且唯若 對任意 $\lambda \in \mathbb{C}$，
$$rank\left[ {\begin{array}{*{20}{c}} {\lambda I - A}\\ C \end{array}} \right] = n$$
注意到上述 Lemma 中，若 $\lambda \notin eig(A)$，則前面 $n$ rows 為 linearly independent ，故我們可已不用檢驗整個複數平面 $\lambda \in \mathbb{C}$，僅僅需要檢驗 $\lambda \in eig(A)$ 的部分即可。故我們得到以下修正引理：

Lemma: Modified Hautus Lemma
一個系統為 observable 若且唯若 對任意 $\lambda \in eig(A)$，
$$rank\left[ {\begin{array}{*{20}{c}} {\lambda I - A}\\ C \end{array}} \right] = n$$