by Chung-Han Hsieh
If you can’t solve a problem, then there is an easier problem you can solve: find it. -George Polya
9/21/2012
9/20/2012
[系統理論] 連續時間 週期訊號的 Fourier Transform Representation
延續前篇
[系統理論] 連續時間 非週期訊號的 Fourier Transform Representation,我們知道 非週期訊號$x(t)$ 若滿足 Dirchlet conditions 則 Fourier Transform 存在,且我們可寫成
\[\left\{ \begin{array}{l}
X\left( {j\omega } \right) = \int_{ - \infty }^\infty {x\left( t \right){e^{ - j\omega t}}dt} \ \ \ \ (1) \\
x\left( t \right) = \frac{1}{{2\pi }}\int_{ - \infty }^\infty {X\left( {j\omega } \right){e^{j\omega t}}d\omega} \ \ \ \ (2)
\end{array} \right.\]上式中 $(1)$ 稱為 $x(t)$ 的 Fourier Transform,$(2)$ 稱為 Inverse Fourier Transform。
事實上,對於週期訊號而言,除了 Fourier Series 之外, 我們亦可對 週期訊號 求解 Fourier Transform 。 那麼該怎麼做呢?
想法: 透過 Impulse function 幫助我們對 Fourier Transform 進行"取樣"
首先我們先做個觀察如下:
考慮一個訊號 $x(t)$ 其 Fourier Transform $X(j \omega)$ 為落在 $\omega = \omega_0$ 且面積為 $2 \pi$ 的單位脈衝函數如下
\[
X(j \omega) = 2 \pi \delta(\omega - \omega_0)
\]現在利用 Inverse Fourier Transform 我們可得回 $x(t)$
\[\begin{array}{l}
x\left( t \right) = \frac{1}{{2\pi }}\int_{ - \infty }^\infty {X\left( {j\omega } \right){e^{j\omega t}}d\omega} \\
\begin{array}{*{20}{c}}
{}&{}
\end{array} = \frac{1}{{2\pi }}\int_{ - \infty }^\infty {2\pi \delta (\omega - {\omega _0}){e^{j\omega t}}d\omega} = {e^{j{\omega _0}t}}
\end{array}
\]上述的結果暗示了我們可以得到 $x(t) = e^{j k \omega_0t}$,此 complex exponential 訊號確實為週期訊號。 現在我們回憶 Fourier Series Representation,週期訊號 $x(t)$ 可以透過 complex exponential 做線性組合。故我們試圖拓展上述想法,目標是如果可以找出一個 Fourier Transform $X(j \omega)$ 使得 $x(t)$ 具有 Complex exponential 做線性組合的形式 (亦即具有 Fourier Series 的形式),我們便大功告成
現在我們拓展上述想法,由於前述 我們利用脈衝函數當作 Fourier Transform 確實可以得回 complex exponential 訊號,故我們繼續沿用此脈衝函數,且更進一步拓展為一組脈衝函數的線性組合看看會有甚麼發現。
故考慮 $x(t)$ 的 Fourier Transform, $X(j \omega)$ 為 一組脈衝函數的線性組合
\[X\left( {j\omega } \right) = \sum\limits_{k = - \infty }^\infty {2\pi {a_k}\delta \left( {\omega - k{\omega _0}} \right)} \]則透過 Inverse Fourier Transform 我們可得
\[\begin{array}{l}
x\left( t \right) = \frac{1}{{2\pi }}\int_{ - \infty }^\infty {X\left( {j\omega } \right){e^{j\omega t}}d\omega} \\
\begin{array}{*{20}{c}}
{}&{}
\end{array} = \frac{1}{{2\pi }}\int_{ - \infty }^\infty {\sum\limits_{k = - \infty }^\infty {2\pi {a_k}\delta \left( {\omega - k{\omega _0}} \right)} {e^{j\omega t}}d\omega} \\
\begin{array}{*{20}{c}}
{}&{}
\end{array} = \sum\limits_{k = - \infty }^\infty {{a_k}} \int_{ - \infty }^\infty {\delta \left( {\omega - k{\omega _0}} \right){e^{j\omega t}}d\omega} \\
\begin{array}{*{20}{c}}
{}&{}
\end{array} = \sum\limits_{k = - \infty }^\infty {{a_k}} {e^{jk{\omega _0}t}}
\end{array}\]上式即為 Fourier Series。
小結:
若 週期函數 $x(t)$ 存在 Fourier Series
\[
x(t) = \sum\limits_{k = - \infty }^\infty {{a_k}} {e^{jk{\omega _0}t}}
\] 則其對應的 Fourier Transform: $X(j \omega)$ 為 一組脈衝函數的線性組合
\[X\left( {j\omega } \right) = \sum\limits_{k = - \infty }^\infty {2\pi {a_k}\delta \left( {\omega - k{\omega _0}} \right)} \]
一般而言,對於週期函數我們可預先求解 Fourier coefficient, $a_k$ ,若需要計算其對應的 Fourier Transform,則直接使用上式
我們現在看一些例子:
Example 1
考慮週期方波訊號如下圖
試求其Fourier Transform $X(j \omega)$。
Solution
首先注意到此方波訊號為週期方波,且滿足 Dirchlet conditions,故存在 Fourier Series。因此我們先求解 Fourier Series Coefficient:
\[\begin{array}{l}
{a_k} = \frac{1}{T}\int_T^{} {x\left( t \right){e^{ - jk{\omega _0}t}}dt} \\
\begin{array}{*{20}{c}}
{}&{}
\end{array} = \frac{1}{T}\int_{ - T/2}^{T/2} {x\left( t \right){e^{ - jk{\omega _0}t}}dt} = \frac{1}{T}\int_{ - {T_1}}^{{T_1}} {{e^{ - jk{\omega _0}t}}dt} \\
\begin{array}{*{20}{c}}
{}&{}
\end{array} = \frac{2}{{k{\omega _0}T}}\frac{{{e^{jk{\omega _0}{T_1}}} - {e^{ - jk{\omega _0}{T_1}}}}}{{2j}} = \frac{2}{{k{\omega _0}T}}\sin k{\omega _0}{T_1}
\end{array}\]且 由 $T = 2 \pi/ \omega_0$ 帶入上式,
\[{a_k} = \frac{1}{{k\pi }}\sin \left( {k{\omega _0}{T_1}} \right), \; k \neq 0 \ \ \ \ (*)
\]且若 $k=0$,可計算得到 $a_0$
\[{a_0} = \frac{1}{T}\int_T^{} {x\left( t \right)dt} = \frac{1}{T}\int_{ - {T_1}}^{{T_1}} {1dt} = \frac{{2{T_1}}}{T} \ \ \ \ (**)
\]有了Fourier Series Coefficients 之後,我們便可計算其對應的 Fourier Transform。現在回憶對於週期訊號的 Fourier Transform 為 面積為 $2 \pi$ 且頻率等分的脈衝函數的線性組合,亦即
\[
X(j \omega) = 2 \pi \sum_{k = - \infty}^{\infty}a_k \delta( \omega - k \omega_0)
\]現在代入我們剛剛算出的 Fourier Series Coefficient,我們可得
\[\begin{array}{l}
X(j\omega ) = 2\pi \sum\limits_{k = - \infty }^\infty {{a_k}} \delta (\omega - k{\omega _0})\\
\begin{array}{*{20}{c}}
{}&{}&{}&{}
\end{array} = 2\pi \sum\limits_{k = - \infty }^\infty {\frac{1}{{k\pi }}\sin \left( {k{\omega _0}{T_1}} \right)} \delta (\omega - k{\omega _0})\\
\begin{array}{*{20}{c}}
{}&{}&{}&{}
\end{array} = 2\sum\limits_{k = - \infty }^\infty {\frac{1}{k}\sin \left( {k{\omega _0}{T_1}} \right)} \delta (\omega - k{\omega _0}) \ \ \ \ (\star)
\end{array}\]上式即為 週期方波的 Fourier Transform。 $\square$
Comments
延續上例,現在我們來看看 Fourier Transform 與 Fourier Series 的差別,令 $T = 4 T_1$,我們用 $(\star)$ 繪製 Fourier Transform 的圖形
接著透過 $(*)$ 與 $(**)$ 我們可繪製 Fourier Series Coefficients 的圖形
其中Fourier Series Coefficient 可由我們先前推出的式子計算而得:
$a_0 = 1/2,$ $a_1 = a_{-1}=1/\pi$, $a_3 = a_{-3}=-1/3\pi$, $a_5 = a_{-5} = 1/5\pi$
注意到 圖2 的橫坐標 $k$ 表示 第 $k$ 個 fundamental frequency, $k \omega_0$。
現在比較兩圖,兩圖可發現 Fourier Transform 對週期方波 不過是透過 脈衝函數 對原本的 "sinc 包烙線" 做取樣 (sampling) 的動作。
圖1 與 圖2 之間差別只有下面兩點:
考慮下列 脈衝週期訊號
\[x\left( t \right) = \sum\limits_{k = - \infty }^\infty {\delta \left( {t - kT} \right)} \]試求 Fourier Series coefficients 與 Fourier transform。
Solution
由於 脈衝週期訊號 $x(t)$ 週期為 $T$,且滿足 Dirchlet condtions,故我們有 Fourier series coefficient:
\[\begin{array}{l}
{a_k} = \frac{1}{T}\int_T^{} {x\left( t \right){e^{ - jk{\omega _0}t}}dt} = \frac{1}{T}\int_{ - T/2}^{T/2} {\delta \left( t \right){e^{ - jk{\omega _0}t}}dt} \\
\begin{array}{*{20}{c}}
{}&{}
\end{array} = \frac{1}{T}\int_{ - T/2}^{T/2} {\delta \left( t \right){e^{ - jk{\omega _0}t}}dt} = \frac{1}{T}\underbrace {\int_{ - \infty }^\infty {\delta \left( t \right){e^{ - jk{\omega _0}t}}dt} }_{ = {e^{ - jk{\omega _0}0}} = 1} = \frac{1}{T}
\end{array}\]接著計算此週期脈衝訊號的 Fourier transform,由前面討論可知週期訊號 $x(t)$ 的 Fourier transform 為
\[X(j\omega ) = \sum\limits_{k = - \infty }^\infty 2 \pi {a_k}\delta (\omega - k{\omega _0}) = \frac{{2\pi }}{T}\sum\limits_{k = - \infty }^\infty {\delta (\omega - k\frac{{2\pi }}{T})} \]
Example 3 (Cosine Function)
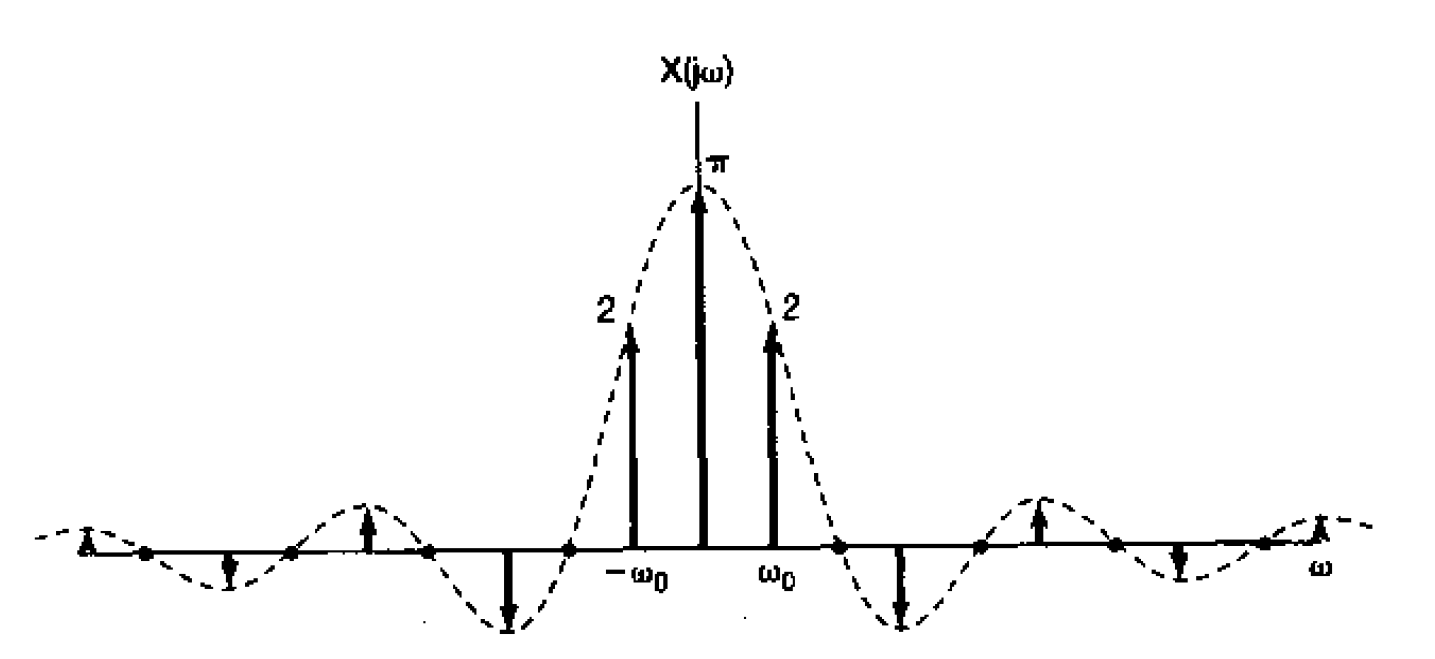
考慮 $x(t) := \cos(\omega_0 t)$,試求 Fourier transform。
Solution
由於 $x(t)$ 為週期訊號,我們可知其 Fourier transform 可表為 脈衝函數的線性組合
\[
X(j \omega) = 2 \pi \sum_{k = -\infty}^{\infty} a_k \delta(\omega - k \omega_0) \ \ \ \ (*)
\] 其中 $a_k$ 為 Fourier series coefficient,由於 $\cos(\omega_0 t)$ 可寫為 complex exponential 如下
\[\cos \left( {{\omega _0}t} \right) = \frac{{{e^{j{\omega _0}t}} + {e^{ - j{\omega _0}t}}}}{2}\] (亦即只有 $k = \pm 1$ 的 Fourier coefficient) 故可知 $a_1 = a_{-1} = 1/2$。現在將此結果帶回 $(*)$ 我們得到
\[\begin{array}{l}
X(j\omega ) = 2\pi \frac{1}{2}\delta (\omega - {\omega _0}) + 2\pi \frac{1}{2}\delta (\omega ++ {\omega _0})\\
\begin{array}{*{20}{c}}
{}&{}&{}
\end{array} = \pi \delta (\omega - {\omega _0}) + \pi \delta (\omega +{\omega _0}) \ \ \ \ \square
\end{array}\]
Example 4 (Scaled Cosine Function)
現在考慮 $x(t) := \cos(\omega_0 t) /a, \; a>0$ 試求其對應的 Fourier transform。
Solution
由 Example 3,我們已知 $\cos(\omega_0 t)$ 的 Fourier transform 為
\[
\pi \delta (\omega - {\omega _0}) + \pi \delta (\omega - {\omega _0})
\] 故 $x(t) = \cos(\omega_0 t) /a $ 的 Fourier transform 由 linearity 可知
\[
X(j \omega) = \frac{1}{a} \left [\pi \delta (\omega - {\omega _0}) + \pi \delta (\omega - {\omega _0})\right] \ \ \ \ \square
\]
Comments:
若我們要求以頻率 $f$ 表示 $(\omega = 2 \pi f)$,則 Example 4 中的結果 變為
\[\begin{array}{l}
X(f) = \frac{1}{a}\left[ {\pi \delta (2\pi f - 2\pi {f_0}) + \pi \delta (2\pi f - 2\pi {f_0})} \right]\;\\
\begin{array}{*{20}{c}}
{}&{}&{}&{}
\end{array} = \frac{1}{a}\left[ {\pi \delta (2\pi \left( {f - {f_0}} \right)) + \pi \delta (2\pi \left( {f - {f_0}} \right))} \right]\;
\end{array}\]利用脈衝函數的 scaling 性質 :
\[
\delta(a t) = \frac{1}{|a|} \delta(t)
\]改寫前式
\[\begin{array}{l}
X(f) = \frac{1}{a}\left[ {\pi \delta (2\pi \left( {f - {f_0}} \right)) + \pi \delta (2\pi \left( {f - {f_0}} \right))} \right]\;\\
\begin{array}{*{20}{c}}
{}&{}&{}&{}
\end{array} = \frac{1}{a}\left[ {\pi \frac{1}{{2\pi }}\delta \left( {f - {f_0}} \right) + \pi \frac{1}{{2\pi }}\delta \left( {f - {f_0}} \right)} \right]\;\\
\begin{array}{*{20}{c}}
{}&{}&{}&{}
\end{array} = \frac{1}{{2a}}\left[ {\delta \left( {f - {f_0}} \right) + \delta \left( {f - {f_0}} \right)} \right]\;
\end{array}\]
ref: A.V. Oppenheim, A. S. Willsky, S. H. Nawab, Signals and Systems
[系統理論] 連續時間 非週期訊號的 Fourier Transform Representation,我們知道 非週期訊號$x(t)$ 若滿足 Dirchlet conditions 則 Fourier Transform 存在,且我們可寫成
\[\left\{ \begin{array}{l}
X\left( {j\omega } \right) = \int_{ - \infty }^\infty {x\left( t \right){e^{ - j\omega t}}dt} \ \ \ \ (1) \\
x\left( t \right) = \frac{1}{{2\pi }}\int_{ - \infty }^\infty {X\left( {j\omega } \right){e^{j\omega t}}d\omega} \ \ \ \ (2)
\end{array} \right.\]上式中 $(1)$ 稱為 $x(t)$ 的 Fourier Transform,$(2)$ 稱為 Inverse Fourier Transform。
事實上,對於週期訊號而言,除了 Fourier Series 之外, 我們亦可對 週期訊號 求解 Fourier Transform 。 那麼該怎麼做呢?
想法: 透過 Impulse function 幫助我們對 Fourier Transform 進行"取樣"
首先我們先做個觀察如下:
考慮一個訊號 $x(t)$ 其 Fourier Transform $X(j \omega)$ 為落在 $\omega = \omega_0$ 且面積為 $2 \pi$ 的單位脈衝函數如下
\[
X(j \omega) = 2 \pi \delta(\omega - \omega_0)
\]現在利用 Inverse Fourier Transform 我們可得回 $x(t)$
\[\begin{array}{l}
x\left( t \right) = \frac{1}{{2\pi }}\int_{ - \infty }^\infty {X\left( {j\omega } \right){e^{j\omega t}}d\omega} \\
\begin{array}{*{20}{c}}
{}&{}
\end{array} = \frac{1}{{2\pi }}\int_{ - \infty }^\infty {2\pi \delta (\omega - {\omega _0}){e^{j\omega t}}d\omega} = {e^{j{\omega _0}t}}
\end{array}
\]上述的結果暗示了我們可以得到 $x(t) = e^{j k \omega_0t}$,此 complex exponential 訊號確實為週期訊號。 現在我們回憶 Fourier Series Representation,週期訊號 $x(t)$ 可以透過 complex exponential 做線性組合。故我們試圖拓展上述想法,目標是如果可以找出一個 Fourier Transform $X(j \omega)$ 使得 $x(t)$ 具有 Complex exponential 做線性組合的形式 (亦即具有 Fourier Series 的形式),我們便大功告成
現在我們拓展上述想法,由於前述 我們利用脈衝函數當作 Fourier Transform 確實可以得回 complex exponential 訊號,故我們繼續沿用此脈衝函數,且更進一步拓展為一組脈衝函數的線性組合看看會有甚麼發現。
故考慮 $x(t)$ 的 Fourier Transform, $X(j \omega)$ 為 一組脈衝函數的線性組合
\[X\left( {j\omega } \right) = \sum\limits_{k = - \infty }^\infty {2\pi {a_k}\delta \left( {\omega - k{\omega _0}} \right)} \]則透過 Inverse Fourier Transform 我們可得
\[\begin{array}{l}
x\left( t \right) = \frac{1}{{2\pi }}\int_{ - \infty }^\infty {X\left( {j\omega } \right){e^{j\omega t}}d\omega} \\
\begin{array}{*{20}{c}}
{}&{}
\end{array} = \frac{1}{{2\pi }}\int_{ - \infty }^\infty {\sum\limits_{k = - \infty }^\infty {2\pi {a_k}\delta \left( {\omega - k{\omega _0}} \right)} {e^{j\omega t}}d\omega} \\
\begin{array}{*{20}{c}}
{}&{}
\end{array} = \sum\limits_{k = - \infty }^\infty {{a_k}} \int_{ - \infty }^\infty {\delta \left( {\omega - k{\omega _0}} \right){e^{j\omega t}}d\omega} \\
\begin{array}{*{20}{c}}
{}&{}
\end{array} = \sum\limits_{k = - \infty }^\infty {{a_k}} {e^{jk{\omega _0}t}}
\end{array}\]上式即為 Fourier Series。
小結:
若 週期函數 $x(t)$ 存在 Fourier Series
\[
x(t) = \sum\limits_{k = - \infty }^\infty {{a_k}} {e^{jk{\omega _0}t}}
\] 則其對應的 Fourier Transform: $X(j \omega)$ 為 一組脈衝函數的線性組合
\[X\left( {j\omega } \right) = \sum\limits_{k = - \infty }^\infty {2\pi {a_k}\delta \left( {\omega - k{\omega _0}} \right)} \]
一般而言,對於週期函數我們可預先求解 Fourier coefficient, $a_k$ ,若需要計算其對應的 Fourier Transform,則直接使用上式
我們現在看一些例子:
Example 1
考慮週期方波訊號如下圖
試求其Fourier Transform $X(j \omega)$。
Solution
首先注意到此方波訊號為週期方波,且滿足 Dirchlet conditions,故存在 Fourier Series。因此我們先求解 Fourier Series Coefficient:
\[\begin{array}{l}
{a_k} = \frac{1}{T}\int_T^{} {x\left( t \right){e^{ - jk{\omega _0}t}}dt} \\
\begin{array}{*{20}{c}}
{}&{}
\end{array} = \frac{1}{T}\int_{ - T/2}^{T/2} {x\left( t \right){e^{ - jk{\omega _0}t}}dt} = \frac{1}{T}\int_{ - {T_1}}^{{T_1}} {{e^{ - jk{\omega _0}t}}dt} \\
\begin{array}{*{20}{c}}
{}&{}
\end{array} = \frac{2}{{k{\omega _0}T}}\frac{{{e^{jk{\omega _0}{T_1}}} - {e^{ - jk{\omega _0}{T_1}}}}}{{2j}} = \frac{2}{{k{\omega _0}T}}\sin k{\omega _0}{T_1}
\end{array}\]且 由 $T = 2 \pi/ \omega_0$ 帶入上式,
\[{a_k} = \frac{1}{{k\pi }}\sin \left( {k{\omega _0}{T_1}} \right), \; k \neq 0 \ \ \ \ (*)
\]且若 $k=0$,可計算得到 $a_0$
\[{a_0} = \frac{1}{T}\int_T^{} {x\left( t \right)dt} = \frac{1}{T}\int_{ - {T_1}}^{{T_1}} {1dt} = \frac{{2{T_1}}}{T} \ \ \ \ (**)
\]有了Fourier Series Coefficients 之後,我們便可計算其對應的 Fourier Transform。現在回憶對於週期訊號的 Fourier Transform 為 面積為 $2 \pi$ 且頻率等分的脈衝函數的線性組合,亦即
\[
X(j \omega) = 2 \pi \sum_{k = - \infty}^{\infty}a_k \delta( \omega - k \omega_0)
\]現在代入我們剛剛算出的 Fourier Series Coefficient,我們可得
\[\begin{array}{l}
X(j\omega ) = 2\pi \sum\limits_{k = - \infty }^\infty {{a_k}} \delta (\omega - k{\omega _0})\\
\begin{array}{*{20}{c}}
{}&{}&{}&{}
\end{array} = 2\pi \sum\limits_{k = - \infty }^\infty {\frac{1}{{k\pi }}\sin \left( {k{\omega _0}{T_1}} \right)} \delta (\omega - k{\omega _0})\\
\begin{array}{*{20}{c}}
{}&{}&{}&{}
\end{array} = 2\sum\limits_{k = - \infty }^\infty {\frac{1}{k}\sin \left( {k{\omega _0}{T_1}} \right)} \delta (\omega - k{\omega _0}) \ \ \ \ (\star)
\end{array}\]上式即為 週期方波的 Fourier Transform。 $\square$
Comments
延續上例,現在我們來看看 Fourier Transform 與 Fourier Series 的差別,令 $T = 4 T_1$,我們用 $(\star)$ 繪製 Fourier Transform 的圖形
圖1. Fourier transform plot for periodic square wave
接著透過 $(*)$ 與 $(**)$ 我們可繪製 Fourier Series Coefficients 的圖形
圖2. Fourier series plot for periodic square wave
$a_0 = 1/2,$ $a_1 = a_{-1}=1/\pi$, $a_3 = a_{-3}=-1/3\pi$, $a_5 = a_{-5} = 1/5\pi$
注意到 圖2 的橫坐標 $k$ 表示 第 $k$ 個 fundamental frequency, $k \omega_0$。
現在比較兩圖,兩圖可發現 Fourier Transform 對週期方波 不過是透過 脈衝函數 對原本的 "sinc 包烙線" 做取樣 (sampling) 的動作。
圖1 與 圖2 之間差別只有下面兩點:
- Fourier transform 圖形採用脈衝函數 (impulse function, $\delta(\cdot)$) 而 Fourier Series 採用條狀圖 (bar graph)。
- Fourier transform 為 Fourier Series 放大 $2\pi$ 倍
考慮下列 脈衝週期訊號
\[x\left( t \right) = \sum\limits_{k = - \infty }^\infty {\delta \left( {t - kT} \right)} \]試求 Fourier Series coefficients 與 Fourier transform。
Solution
由於 脈衝週期訊號 $x(t)$ 週期為 $T$,且滿足 Dirchlet condtions,故我們有 Fourier series coefficient:
\[\begin{array}{l}
{a_k} = \frac{1}{T}\int_T^{} {x\left( t \right){e^{ - jk{\omega _0}t}}dt} = \frac{1}{T}\int_{ - T/2}^{T/2} {\delta \left( t \right){e^{ - jk{\omega _0}t}}dt} \\
\begin{array}{*{20}{c}}
{}&{}
\end{array} = \frac{1}{T}\int_{ - T/2}^{T/2} {\delta \left( t \right){e^{ - jk{\omega _0}t}}dt} = \frac{1}{T}\underbrace {\int_{ - \infty }^\infty {\delta \left( t \right){e^{ - jk{\omega _0}t}}dt} }_{ = {e^{ - jk{\omega _0}0}} = 1} = \frac{1}{T}
\end{array}\]接著計算此週期脈衝訊號的 Fourier transform,由前面討論可知週期訊號 $x(t)$ 的 Fourier transform 為
\[X(j\omega ) = \sum\limits_{k = - \infty }^\infty 2 \pi {a_k}\delta (\omega - k{\omega _0}) = \frac{{2\pi }}{T}\sum\limits_{k = - \infty }^\infty {\delta (\omega - k\frac{{2\pi }}{T})} \]
Example 3 (Cosine Function)
考慮 $x(t) := \cos(\omega_0 t)$,試求 Fourier transform。
Solution
由於 $x(t)$ 為週期訊號,我們可知其 Fourier transform 可表為 脈衝函數的線性組合
\[
X(j \omega) = 2 \pi \sum_{k = -\infty}^{\infty} a_k \delta(\omega - k \omega_0) \ \ \ \ (*)
\] 其中 $a_k$ 為 Fourier series coefficient,由於 $\cos(\omega_0 t)$ 可寫為 complex exponential 如下
\[\cos \left( {{\omega _0}t} \right) = \frac{{{e^{j{\omega _0}t}} + {e^{ - j{\omega _0}t}}}}{2}\] (亦即只有 $k = \pm 1$ 的 Fourier coefficient) 故可知 $a_1 = a_{-1} = 1/2$。現在將此結果帶回 $(*)$ 我們得到
\[\begin{array}{l}
X(j\omega ) = 2\pi \frac{1}{2}\delta (\omega - {\omega _0}) + 2\pi \frac{1}{2}\delta (\omega ++ {\omega _0})\\
\begin{array}{*{20}{c}}
{}&{}&{}
\end{array} = \pi \delta (\omega - {\omega _0}) + \pi \delta (\omega +{\omega _0}) \ \ \ \ \square
\end{array}\]
Example 4 (Scaled Cosine Function)
現在考慮 $x(t) := \cos(\omega_0 t) /a, \; a>0$ 試求其對應的 Fourier transform。
Solution
由 Example 3,我們已知 $\cos(\omega_0 t)$ 的 Fourier transform 為
\[
\pi \delta (\omega - {\omega _0}) + \pi \delta (\omega - {\omega _0})
\] 故 $x(t) = \cos(\omega_0 t) /a $ 的 Fourier transform 由 linearity 可知
\[
X(j \omega) = \frac{1}{a} \left [\pi \delta (\omega - {\omega _0}) + \pi \delta (\omega - {\omega _0})\right] \ \ \ \ \square
\]
Comments:
若我們要求以頻率 $f$ 表示 $(\omega = 2 \pi f)$,則 Example 4 中的結果 變為
\[\begin{array}{l}
X(f) = \frac{1}{a}\left[ {\pi \delta (2\pi f - 2\pi {f_0}) + \pi \delta (2\pi f - 2\pi {f_0})} \right]\;\\
\begin{array}{*{20}{c}}
{}&{}&{}&{}
\end{array} = \frac{1}{a}\left[ {\pi \delta (2\pi \left( {f - {f_0}} \right)) + \pi \delta (2\pi \left( {f - {f_0}} \right))} \right]\;
\end{array}\]利用脈衝函數的 scaling 性質 :
\[
\delta(a t) = \frac{1}{|a|} \delta(t)
\]改寫前式
\[\begin{array}{l}
X(f) = \frac{1}{a}\left[ {\pi \delta (2\pi \left( {f - {f_0}} \right)) + \pi \delta (2\pi \left( {f - {f_0}} \right))} \right]\;\\
\begin{array}{*{20}{c}}
{}&{}&{}&{}
\end{array} = \frac{1}{a}\left[ {\pi \frac{1}{{2\pi }}\delta \left( {f - {f_0}} \right) + \pi \frac{1}{{2\pi }}\delta \left( {f - {f_0}} \right)} \right]\;\\
\begin{array}{*{20}{c}}
{}&{}&{}&{}
\end{array} = \frac{1}{{2a}}\left[ {\delta \left( {f - {f_0}} \right) + \delta \left( {f - {f_0}} \right)} \right]\;
\end{array}\]
ref: A.V. Oppenheim, A. S. Willsky, S. H. Nawab, Signals and Systems
訂閱:
文章 (Atom)
[最佳化] C^2 函數一階逼近的餘項積分表示
令 $f: \mathbb{R}^m \to \mathbb{R}$ 為 $C^2$-函數。對 $f$ 在 $y$ 附近使用一階泰勒展開: \[ T_y(x) := f(y) + \nabla f(y)^\top (x - y) \] 則其餘項 $R(x,y)$ 訂為 $$R(...
-
數學上的 if and only if ( 此文不討論邏輯學中的 if and only if,只討論數學上的 if and only if。) 中文翻譯叫做 若且唯若 (or 當且僅當) , 記得當初剛接觸這個詞彙的時候,我是完全不明白到底是甚麼意思,查了翻譯也是愛...
-
這次要介紹的是數學上一個重要的概念: Norm: 一般翻譯成 範數 (在英語中 norm 有規範的意思,比如我們說normalization就是把某種東西/物品/事件 做 正規化,也就是加上規範使其正常化),不過個人認為其實翻譯成 範數 也是看不懂的...這邊建議把 No...
-
半導體中的電流是由電子(electron)及電洞(hole)兩種載子(carrier)移動所產生 載子移動的方式: 擴散(diffusion) $\Rightarrow$ 擴散電流 (不受外力電場作用) 飄移(drift) $\Rightarrow$ 飄移電流 (受外...