Preliminary
回憶若 $x$ 為 mean $m$ 且 variance $\sigma^2$ 的 Normal 隨機變數 則 我們表示為 $x \sim N(m, \sigma^2)$ 。其 probability density function 可記做
\[
\frac{1}{\sqrt{2 \pi} \sigma} \exp(\frac{-1}{2 \sigma^2}(x-m)^2)
\]現在若我們拓展上述結果到 多個隨機變數 (又稱 random vector 隨機向量) 的情況,令 $x$ 為Normal 隨機向量 記做
\[
x \sim N(m,P); \;\;
p_x(x) := n(x,m,P)
\]上述符號 表示 $x$ 為 normal distributed 且 mean vector $m$ 與 convariance matrix $P$。另外 $n(x,m,P)$ 表示 normal probability density function
\[\;n\left( {x,m,P} \right): = \frac{1}{{{{\left( {2\pi } \right)}^{n/2}}{{\left( {\det P} \right)}^{1/2}}}}\exp \left( { - \frac{1}{2}{{\left( {x - m} \right)}^T}{P^{ - 1}}\left( {x - m} \right)} \right)\]
Comment:
若 $x \in \mathbb{R}^n$ 則 mean vector $m \in \mathbb{R}^n$ 且 convariance matrix $P \in \mathbb{R}^{n \times n}$ 且為 實數 對稱 正定 矩陣 (正定條件用以確保 $P^{-1}$ 存在,使得上述的 probability density function 可以被定義)。若 $P$ 不為對 正定 我們稱為 singular normal distribution 或稱 degenerate normal。
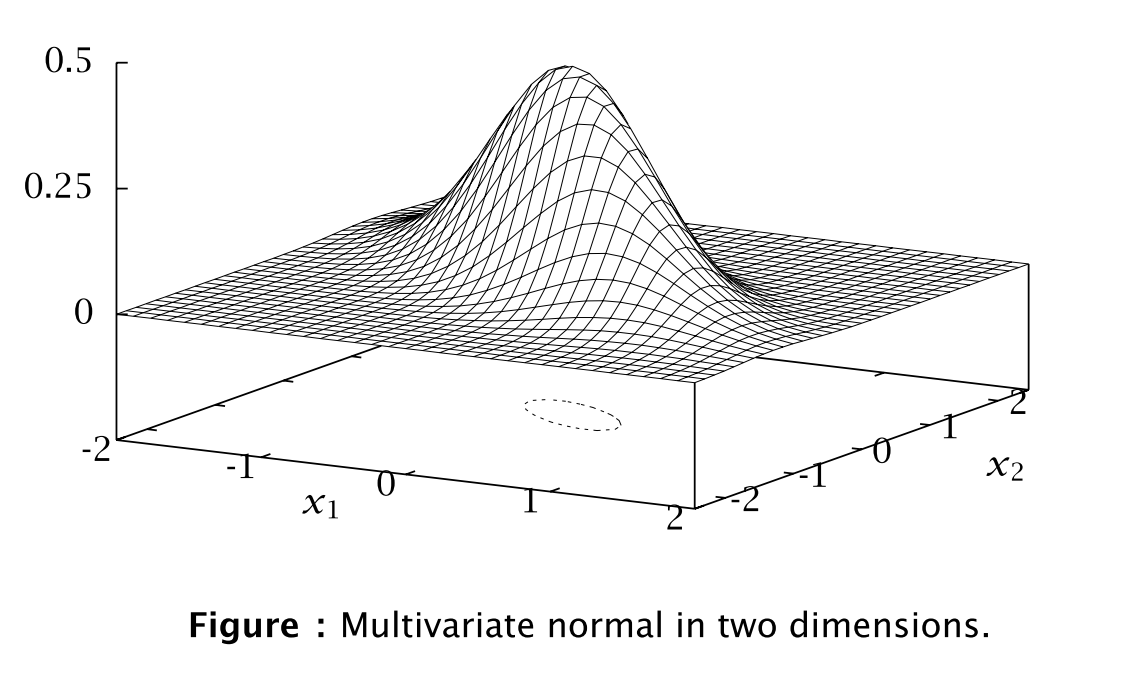
Example
若 $n=2$ 則我們可以繪製 normal density function; 比如說
\[m = \left[ {\begin{array}{*{20}{c}}
0\\
0
\end{array}} \right];\begin{array}{*{20}{c}}
{}&{}
\end{array}{P^{ - 1}} = \left[ {\begin{array}{*{20}{c}}
{3.5}&{2.5}\\
{2.5}&{4.0}
\end{array}} \right]\]則我們可繪製
現在我們看幾個 之後會使用到的基本結果:
================
FACT 1: Joint independent normals
若隨機向量 $x \sim N(m_x,P_x)$ 與 $y \sim N(m_y,P_y)$ 為 normally distributed 且 彼此互為獨立,則其 joint density $p_{x,y}(x,y)$ 如下
\[
p_{x,y}(x,y) = p_{x}(x)p_{y}(y)=n(x,m_x,P_x) \cdot n(y,m_y,P_y)
\]且
\[\left[ {\begin{array}{*{20}{c}}
x\\
y
\end{array}} \right] \sim N\left( {\left[ {\begin{array}{*{20}{c}}
{{m_x}}\\
{{m_y}}
\end{array}} \right],\left[ {\begin{array}{*{20}{c}}
{{P_x}}&0\\
0&{{P_y}}
\end{array}} \right]} \right)\]================
================
FACT 2: Linear Transformation of a normal
若 $x \sim N(m, P)$ 且 $y$ 為 $x$ 的線性轉換;亦即對任意矩陣 $A$, $y = Ax$ 則
\[
y \sim N(Am , APA^T)
\]================
================
FACT 3: Conditional of a joint normal
若 $x,y$ 為 jointly normal distributed (no independent assumption)
\[\left[ {\begin{array}{*{20}{c}}
x\\
y
\end{array}} \right]\sim N\left( {\left[ {\begin{array}{*{20}{c}}
{{m_x}}\\
{{m_y}}
\end{array}} \right],\left[ {\begin{array}{*{20}{c}}
{{P_x}}&{{P_{xy}}}\\
{{P_{yx}}}&{{P_y}}
\end{array}} \right]} \right)\]則 conditional density of $x$ given $y$ 仍為 Normal 亦即
\[
(x|y) \sim N(m,P)
\]其 probability density function 為 $ p_{x|y} (x|y) = n(x,m,P)$ 其中 conditional mean vector $m$ 與 conditional convariance matrix $P$ 分別為
\[\begin{array}{l}
m = {m_x} + {P_{xy}}P_y^{ - 1}(y - {m_y})\\
P = {P_x} - {P_{xy}}P_y^{ - 1}{P_{yx}}
\end{array}\]================
注意到上式中 conditional mean $m$ 為 random vector (depends on $y$) 。
Proof:
回憶 conditional density of $x$ given y 定義
\[
p_{x|y}(x,y) := \frac{p_{x,y}(x,y)}{p_y(y)}
\]注意到 $(x,y)$ 為 joint normal 故我們有
\[\small \begin{array}{l}
{p_y}\left( y \right): = \frac{1}{{{{\left( {2\pi } \right)}^{{n_y}/2}}{{\left( {\det {P_y}} \right)}^{1/2}}}}\exp \left( { - \frac{1}{2}{{\left( {y - {m_y}} \right)}^T}{P_y}^{ - 1}\left( {y - {m_y}} \right)} \right)\\
{p_{x,y}}\left( {x,y} \right): = \frac{1}{{{{\left( {2\pi } \right)}^{\left( {{n_x} + {n_y}} \right)/2}}{{\left( {\det \left[ {\begin{array}{*{20}{c}}
{{P_x}}&{{P_{xy}}}\\
{{P_{yx}}}&{{P_y}}
\end{array}} \right]} \right)}^{1/2}}}}\exp \left( { - \frac{1}{2}{{\left[ {\begin{array}{*{20}{c}}
{x - {m_x}}\\
{y - {m_y}}
\end{array}} \right]}^T}{{\left[ {\begin{array}{*{20}{c}}
{{P_x}}&{{P_{xy}}}\\
{{P_{yx}}}&{{P_y}}
\end{array}} \right]}^{ - 1}}\left[ {\begin{array}{*{20}{c}}
{x - {m_x}}\\
{y - {m_y}}
\end{array}} \right]} \right)
\end{array}\]亦即
\[\begin{array}{l}
{p_{x|y}}\left( {x|y} \right) = \frac{{{p_{x,y}}\left( {x,y} \right)}}{{{p_y}\left( y \right)}}\\
\begin{array}{*{20}{c}}
{}&{}&{}&{}
\end{array} = \frac{{\frac{1}{{{{\left( {2\pi } \right)}^{\left( {{n_x} + {n_y}} \right)/2}}{{\left( {\det \left[ {\begin{array}{*{20}{c}}
{{P_x}}&{{P_{xy}}}\\
{{P_{yx}}}&{{P_y}}
\end{array}} \right]} \right)}^{1/2}}}}\exp \left( { - \frac{1}{2}{{\left[ {\begin{array}{*{20}{c}}
{x - {m_x}}\\
{y - {m_y}}
\end{array}} \right]}^T}{{\left[ {\begin{array}{*{20}{c}}
{{P_x}}&{{P_{xy}}}\\
{{P_{yx}}}&{{P_y}}
\end{array}} \right]}^{ - 1}}\left[ {\begin{array}{*{20}{c}}
{x - {m_x}}\\
{y - {m_y}}
\end{array}} \right]} \right)}}{{\frac{1}{{{{\left( {2\pi } \right)}^{{n_y}/2}}{{\left( {\det {P_y}} \right)}^{1/2}}}}\exp \left( { - \frac{1}{2}{{\left( {y - {m_y}} \right)}^T}{P_y}^{ - 1}\left( {y - {m_y}} \right)} \right)}}\\
\begin{array}{*{20}{c}}
{}&{}&{}&{}
\end{array} = \frac{{{{\left( {\det {P_y}} \right)}^{1/2}}\exp \left( { - \frac{1}{2}\left( {{{\left[ {\begin{array}{*{20}{c}}
{x - {m_x}}\\
{y - {m_y}}
\end{array}} \right]}^T}{{\left[ {\begin{array}{*{20}{c}}
{{P_x}}&{{P_{xy}}}\\
{{P_{yx}}}&{{P_y}}
\end{array}} \right]}^{ - 1}}\left[ {\begin{array}{*{20}{c}}
{x - {m_x}}\\
{y - {m_y}}
\end{array}} \right] - {{\left( {y - {m_y}} \right)}^T}{P_y}^{ - 1}\left( {y - {m_y}} \right)} \right)} \right)}}{{{{\left( {2\pi } \right)}^{{n_x}/2}}{{\left( {\det \left[ {\begin{array}{*{20}{c}}
{{P_x}}&{{P_{xy}}}\\
{{P_{yx}}}&{{P_y}}
\end{array}} \right]} \right)}^{1/2}}}}
\end{array}\]注意到若我們取 $P:= P_x - P_{xy}P_y^{-1}P_{yx}$ 則 利用 Matrix inversion Lemma 可知
\[{\left[ {\begin{array}{*{20}{c}}
{{P_x}}&{{P_{xy}}}\\
{{P_{yx}}}&{{P_y}}
\end{array}} \right]^{ - 1}} = \left[ {\begin{array}{*{20}{c}}
{{P^{ - 1}}}&{ - {P^{ - 1}}{P_{xy}}P_y^{ - 1}}\\
{ - P_y^{ - 1}{P_{yx}}{P^{ - 1}}}&{P_y^{ - 1} + P_y^{ - 1}{P_{yx}}{P^{ - 1}}{P_{xy}}P_y^{ - 1}}
\end{array}} \right]\]將此結果帶回我們可得
\[\begin{array}{l}
{p_{x|y}}\left( {x|y} \right) = \frac{{{p_{x,y}}\left( {x,y} \right)}}{{{p_y}\left( y \right)}}\\
\begin{array}{*{20}{c}}
{}&{}&{}
\end{array} = \frac{{{{\left( {\det {P_y}} \right)}^{1/2}}\exp \left( { - \frac{1}{2}\left( \begin{array}{l}
{\left( {x - {m_x}} \right)^T}{P^{ - 1}}\left( {x - {m_x}} \right) - 2{\left( {y - {m_y}} \right)^T}P_y^{ - 1}{P_{yx}}{P^{ - 1}}\left( {x - {m_x}} \right)\\
\begin{array}{*{20}{c}}
{}&{}
\end{array} + {\left( {y - {m_y}} \right)^T}\left( {P_y^{ - 1}{P_{yx}}{P^{ - 1}}{P_{xy}}P_y^{ - 1}} \right)\left( {y - {m_y}} \right)
\end{array} \right)} \right)}}{{{{\left( {2\pi } \right)}^{{n_x}/2}}{{\left( {\det \left[ {\begin{array}{*{20}{c}}
{{P_x}}&{{P_{xy}}}\\
{{P_{yx}}}&{{P_y}}
\end{array}} \right]} \right)}^{1/2}}}}\\
\begin{array}{*{20}{c}}
{}&{}&{}
\end{array} = \frac{{{{\left( {\det {P_y}} \right)}^{1/2}}\exp \left( { - \frac{1}{2}\left( {{{\left[ {{{\left( {x - {m_x}} \right)}^T} - {P_{xy}}P_y^{ - 1}\left( {y - {m_y}} \right)} \right]}^T}{P^{ - 1}}\left[ {{{\left( {x - {m_x}} \right)}^T} - {P_{xy}}P_y^{ - 1}\left( {y - {m_y}} \right)} \right]} \right)} \right)}}{{{{\left( {2\pi } \right)}^{{n_x}/2}}{{\left( {\det \left[ {\begin{array}{*{20}{c}}
{{P_x}}&{{P_{xy}}}\\
{{P_{yx}}}&{{P_y}}
\end{array}} \right]} \right)}^{1/2}}}}\\
\begin{array}{*{20}{c}}
{}&{}&{}
\end{array} = \frac{{{{\left( {\det {P_y}} \right)}^{1/2}}\exp \left( { - \frac{1}{2}\left( {{{\left[ {\left( {x - {m_x}} \right) - {P_{xy}}P_y^{ - 1}\left( {y - {m_y}} \right)} \right]}^T}{P^{ - 1}}\left[ {\left( {x - {m_x}} \right) - {P_{xy}}P_y^{ - 1}\left( {y - {m_y}} \right)} \right]} \right)} \right)}}{{{{\left( {2\pi } \right)}^{{n_x}/2}}{{\left( {\det \left[ {\begin{array}{*{20}{c}}
{{P_x}}&{{P_{xy}}}\\
{{P_{yx}}}&{{P_y}}
\end{array}} \right]} \right)}^{1/2}}}}
\end{array}\]接著令 $m := m_x + P_{xy} P_y^{-1}(y-m_y)$ 可得
\[{p_{x|y}}\left( {x|y} \right) = \frac{{{p_{x,y}}\left( {x,y} \right)}}{{{p_y}\left( y \right)}} = \frac{{{{\left( {\det {P_y}} \right)}^{1/2}}\exp \left( { - \frac{1}{2}{{\left( {x - m} \right)}^T}{P^{ - 1}}\left( {x - m} \right)} \right)}}{{{{\left( {2\pi } \right)}^{{n_x}/2}}{{\left( {\det \left[ {\begin{array}{*{20}{c}}
{{P_x}}&{{P_{xy}}}\\
{{P_{yx}}}&{{P_y}}
\end{array}} \right]} \right)}^{1/2}}}}\]注意到
\[\det \left[ {\begin{array}{*{20}{c}}
{{P_x}}&{{P_{xy}}}\\
{{P_{yx}}}&{{P_y}}
\end{array}} \right] = \det {P_y}\det P\]故可得
\[{p_{x|y}}\left( {x|y} \right) = \frac{1}{{{{\left( {2\pi } \right)}^{{n_x}/2}}{{\left( {\det P} \right)}^{1/2}}}}\exp \left( { - \frac{1}{2}{{\left( {x - m} \right)}^T}{P^{ - 1}}\left( {x - m} \right)} \right) = n(x,m,P) \ \ \ \ \ \square
\]
如果要推導 最佳估測器 我們需要上述結果衍生:
================
FACT 1': Joint independent normals
若 $p_{x|z} (x|z) = n(x, m_x, P_x)$ 為 normal ,令 $y \sim N(m_y, P_y)$ 且 與 $x,z$ 彼此獨立 則 conditional joint density of $(x,y)$ given $z$ 為
\[{p_{x,y|z}}\left( {\left[ {\begin{array}{*{20}{c}}
x\\
y
\end{array}} \right]|z} \right) = n\left( {\left[ {\begin{array}{*{20}{c}}
x\\
y
\end{array}} \right],\left[ {\begin{array}{*{20}{c}}
{{m_x}}\\
{{m_y}}
\end{array}} \right],\left[ {\begin{array}{*{20}{c}}
{{P_x}}&0\\
0&{{P_y}}
\end{array}} \right]} \right)\]================
================
FACT 2': Linear Transformation of a Normal
若 $p_{x|z}(x|z)= n(x,m, P)$ 且 $y$ 為 $x$ 的線性轉換;亦即 $y = Ax$ 則
\[{p_{y|z}}(y|z) = n(y,Am,AP{A^T})\]================
================
FACT 3': Conditional of a joint normal
若 $x,y$ 為 jointly normal distributed (no independent assumption)
\[{p_{x,y|z}}\left( {\left[ {\begin{array}{*{20}{c}}
x\\
y
\end{array}} \right]|z} \right) = n\left( {\left[ {\begin{array}{*{20}{c}}
x\\
y
\end{array}} \right],\left[ {\begin{array}{*{20}{c}}
{{m_x}}\\
{{m_y}}
\end{array}} \right],\left[ {\begin{array}{*{20}{c}}
{{P_x}}&{{P_{xy}}}\\
{{P_{yx}}}&{{P_y}}
\end{array}} \right]} \right)\]則 conditional density of $x$ given $y,z$ 仍為 Normal ,記為
\[
p_{x|y,z} (x|y,z) = n(x,m,P)
\]其中 conditional mean vector $m$ 與 conditional convariance matrix $P$ 分別為
\[\begin{array}{l}
m = {m_x} + {P_{xy}}P_y^{ - 1}(y - {m_y})\\
P = {P_x} - {P_{xy}}P_y^{ - 1}{P_{yx}}
\end{array}\]
================
Proof:
由 conditional density of $x$ given $y,z$ 定義可知
\[{p_{x|y,z}}\left( {x|y,z} \right) = \frac{{{p_{x,y,z}}\left( {x,y,z} \right)}}{{{p_{y,z}}\left( {y,z} \right)}}\]現在對等號右方 分子分母同乘 $p(z)$ 可得
\[\begin{array}{l} {p_{x|y,z}}\left( {x|y,z} \right) = \frac{{{p_{x,y,z}}\left( {x,y,z} \right)}}{{{p_{y,z}}\left( {y,z} \right)}}\\ \begin{array}{*{20}{c}} {}&{}&{} \end{array} = \frac{{{p_{x,y,z}}\left( {x,y,z} \right)}}{{{p_z}\left( z \right)}}\frac{{{p_z}\left( z \right)}}{{{p_{y,z}}\left( {y,z} \right)}}\\ \begin{array}{*{20}{c}} {}&{}&{} \end{array} = {p_{x,y|z}}\left( {x,y|z} \right) \cdot \frac{1}{{{p_{y|z}}\left( {y|z} \right)}} \end{array}\]則由先前 FACT 3 可計算 $p(y,z)$ 並且帶入 $p(x,y|z)$ 即可求得所求。$\square$
ref: J. B. Rawlings and D. Q. Mayne, "Model Predictive Control: Theory and Design".
若 $x,y$ 為 jointly normal distributed (no independent assumption)
\[{p_{x,y|z}}\left( {\left[ {\begin{array}{*{20}{c}}
x\\
y
\end{array}} \right]|z} \right) = n\left( {\left[ {\begin{array}{*{20}{c}}
x\\
y
\end{array}} \right],\left[ {\begin{array}{*{20}{c}}
{{m_x}}\\
{{m_y}}
\end{array}} \right],\left[ {\begin{array}{*{20}{c}}
{{P_x}}&{{P_{xy}}}\\
{{P_{yx}}}&{{P_y}}
\end{array}} \right]} \right)\]則 conditional density of $x$ given $y,z$ 仍為 Normal ,記為
\[
p_{x|y,z} (x|y,z) = n(x,m,P)
\]其中 conditional mean vector $m$ 與 conditional convariance matrix $P$ 分別為
\[\begin{array}{l}
m = {m_x} + {P_{xy}}P_y^{ - 1}(y - {m_y})\\
P = {P_x} - {P_{xy}}P_y^{ - 1}{P_{yx}}
\end{array}\]
================
Proof:
由 conditional density of $x$ given $y,z$ 定義可知
\[{p_{x|y,z}}\left( {x|y,z} \right) = \frac{{{p_{x,y,z}}\left( {x,y,z} \right)}}{{{p_{y,z}}\left( {y,z} \right)}}\]現在對等號右方 分子分母同乘 $p(z)$ 可得
\[\begin{array}{l} {p_{x|y,z}}\left( {x|y,z} \right) = \frac{{{p_{x,y,z}}\left( {x,y,z} \right)}}{{{p_{y,z}}\left( {y,z} \right)}}\\ \begin{array}{*{20}{c}} {}&{}&{} \end{array} = \frac{{{p_{x,y,z}}\left( {x,y,z} \right)}}{{{p_z}\left( z \right)}}\frac{{{p_z}\left( z \right)}}{{{p_{y,z}}\left( {y,z} \right)}}\\ \begin{array}{*{20}{c}} {}&{}&{} \end{array} = {p_{x,y|z}}\left( {x,y|z} \right) \cdot \frac{1}{{{p_{y|z}}\left( {y|z} \right)}} \end{array}\]則由先前 FACT 3 可計算 $p(y,z)$ 並且帶入 $p(x,y|z)$ 即可求得所求。$\square$
ref: J. B. Rawlings and D. Q. Mayne, "Model Predictive Control: Theory and Design".


沒有留言:
張貼留言