稱作 風險中性定價 (Risk-Neutral Pricing)。
簡單說就是我們假設一個新世界,在這個世界中的投資人都為風險中性。
這是甚麼意思呢?
真實世界中,投資人大多為風險趨避者 (Risk-Averse);亦即投資人不喜歡風險。如果一旦有風險產生,投資人會要求額外的報酬當作補償 (風險溢價 Risk premium);但風險中性世界的假設是投資人對風險都持中性態度,亦即對風險並不關心。也就是說 若我們處在一個世界是投資者 對風險 不要求 任何額外的補償。則稱此世界為 風險中性 (Risk-Neutral) 世界
則我們可以定義 風險中性機率 $P$ 為風險中性世界中股價上漲的機率
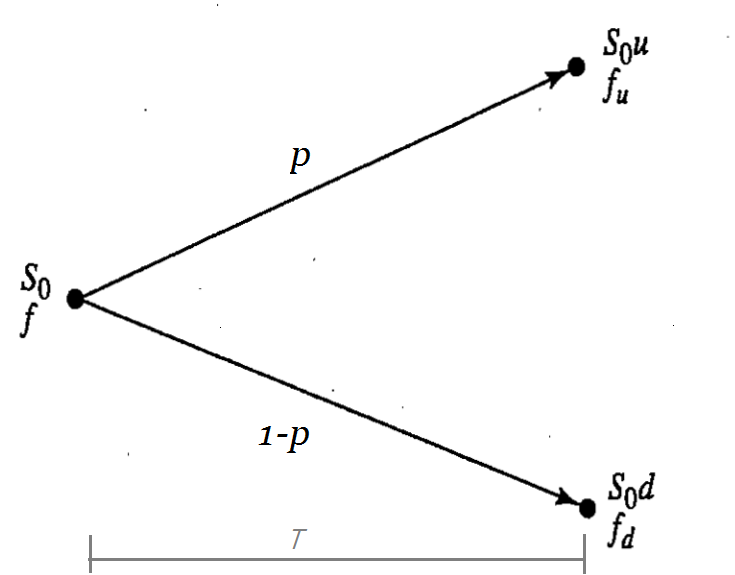
現在考慮下面二項樹
上圖表示在 今日股價為 $S_0$ ,並且考慮在到期時間 $T$ 時,有機率 $P$ 預期股價會上漲成 $S_0 \cdot u$;或者有機率 $(1-P)$ 預期股價會下跌成 $S_0 \cdot d$
NOTE: 注意到上述的 $P$ 為前述定義的風險中性機率。
那麼對於 在到期時間 $T$ 時候的預期股價 $E\left[ {{S_T}} \right] $ 可以寫做:
\[E\left[ {{S_T}} \right] = {S_0}{e^{rT}} = P \cdot \left( {{S_0}u} \right) + (1 - P) \cdot {S_0}d
\]那麼我們可以把 今日股價 $S_0$ 寫成 對到期時間$T$時候,預期股價收益的折現:
\[
{S_0} = \left( {P \cdot \left( {{S_0}u} \right) + (1 - P) \cdot {S_0}d} \right){e^{ - rT}}
\] 由上式我們可以推得 風險中性機率 $P$ 如下:
\[
\Rightarrow P = \frac{{{e^{rT}} - d}}{{u - d}}
\]同樣的,我們也可以透過折現計算 今日 預期選擇權的價格 為 預期收益的折現:
\[
f = \left( {P \cdot {f_u} + (1 - P) \cdot {f_d}} \right){e^{ - rT}} \ \ \ \ (*)
\]
Comment:
1. 風險中性定價方法在計算選擇權價格 較 二項樹求解法容易 (但兩者等價)。因為我們只需先解得 風險中性機率 $P$ 再帶入 $(*)$ 即可求解 $f$。
2. 風險中性機率 $P$ 與真實世界中 股票上漲的機率並不相同!
現在我們考慮一個新的問題:
如果考慮 配發股息情況該如何修正風險中性機率??
考慮與上圖相同的一步 二項樹模型:
其中 $S_0$ 為當前股價,$u$ 為上升因子, $d$ 為下降因子,$f_u$ 為如果股價上升到 $S_u$ 所對應的選擇權價格,$f_d$ 為如果股價下跌到 $S_d$ 所對應的選擇權價格,且給定 $r$ 無風險年利率以連續複利計,$T$ 為到期時間 (以年計算)。則原本不考慮配發股息的風險中性機率 ( Risk-Neutral Probability) $P$ 為
\[
S_0 = (S_0 u P + S_0 d (1-P)) e^{-rT}
\]故整理上式,可得 Risk-Neutral Probability $P$ 為
\[P = \frac{{{e^{rT}} - d}}{{u - d}}
\]
但是現在如果我們考慮標的股票有配發股息的情況,且股息配發為連續複利 $q$ (continuous dividend yield),則原本的 Risk-Neutral Probability 需進行修正:
\[
S_0 e^{-qT}= (S_0 u P + S_0 d (1-P)) e^{-rT}
\]故 考慮配發連續複利股息的 Risk-Neutral Probability 為
\[P = \frac{{{e^{\left( {r - q} \right)T}} - d}}{{u - d}}\]
注意到上述的 Risk-Neutral Probability 求解 option price 的方法跟之前我們介紹的 Binomial Pricing Method 求出的 Option Price 等價,我們現在看個例子來展示此想法:
Example (Equivalent Pricing Approach)
考慮當前股價 $40$,且已知三個月後股價要麼為 $45$ 或者 $35$,且無風險年利率為 $8%$ 以每三個月複利計算,現在是計算 三個月到期且執行價格為 $40$ 的 European Put Option 的合理價格。並且驗證 Risk-Neutral pricing 與 No-arbitrage argument 答案相等。
Solution
首先改寫已知資訊:
\[
S_0 =40, S_0 u=45, S_0 d=35, r_m:=r_{\text{quarterly}}= 0.08, K=40, T=3/12
\] 我們可繪製如前所敘的 Binomial Tree
注意到此題的利率為 每三個月複利計算,故我們需先將此無風險改為連續複利 $r_c$的形式利用轉換式: (有興趣的讀者請參考 [投資理論] Interest Rates and Continuous Compounding.)
\[
{\left( {1 + \frac{{{r_m}}}{m}} \right)^m} = {e^{{r_c}}}
\] 其中 $m$ 為每年複利計算次數,由題目可知為每三個月計算一次,故一年計算複利 4次;亦即 $m=4$,將此參數帶入上述轉換利率式可得連續複利的無風險利率 $r_c$
\[\begin{array}{l}
{\left( {1 + \frac{{0.08}}{4}} \right)^4} = {e^{{r_c}}}\\
\Rightarrow {r_c} = 0.0792
\end{array}
\] 有了 $r_c$ 我們可開始計算 Risk-Neutral Probability
\[\begin{array}{l}
{S_0} = ({S_0}uP + {S_0}d(1 - P)){e^{ - {r_c}T}}\\
\Rightarrow 40 = (45P + 35(1 - P)){e^{ - 0.0792 \times \frac{3}{{12}}}}\\
\Rightarrow P = 0.58
\end{array}
\] 再者由於此為 Put option,故
\[\left\{ \begin{array}{l}
{f_u} = \max \left\{ {K - {S_0}u,0} \right\} = \max \left\{ {40 - 45,0} \right\} = 0\\
{f_d} = \max \left\{ {K - {S_0}d,0} \right\} = \max \left\{ {40 - 35,0} \right\} = 5
\end{array} \right.
\]現在我們可以計算選擇權價格 $f$:
\[\begin{array}{l}
f = \left[ {{f_u}P + {f_d}\left( {1 - P} \right)} \right]{e^{ - rT}}\\
\Rightarrow f = \left[ {0 \times 0.58 + 5 \times \left( {1 - 0.58} \right)} \right]{e^{ - 0.0792 \times \frac{3}{{12}}}}\\
\Rightarrow f = 2.0588
\end{array}\]
現在我們利用 Binomial No-Arbitrage Method:
建構一無風險投資組合:
買入 $\Delta$ 股股票
借入 $B$ 元 債卷
且上述的無風險投資組合必須複製選擇權的payoff,則我們可得
\[\begin{array}{l}
\left\{ \begin{array}{l}
{S_0}u\Delta + B{e^{rT}} = {f_u}\\
{S_0}d\Delta + B{e^{rT}} = {f_d}
\end{array} \right. \Rightarrow \left\{ \begin{array}{l}
45\Delta + B{e^{0.0792 \times \frac{3}{{12}}}} = 0\\
35\Delta + B{e^{0.0792 \times \frac{3}{{12}}}} = 5
\end{array} \right.\\
\Rightarrow \left\{ \begin{array}{l}
\Delta = - 0.5\\
B = 22.0589
\end{array} \right.
\end{array}\]
故可知需要 賣出 $\Delta = 0.5$ 股票,且借入 $B=22.0589$ 元,且 put option 的價格為
\[
f = S_0 \Delta + B = 40 (-0.5) + 22.0589 =2.0589
\] 上述答案與我們使用 Risk-Neutral Probability 所求的答案相等。 $\square$
ref: John C. Hull, Options, Futures and Other Derivatives 7th.




沒有留言:
張貼留言