[衍生商品] 淺談 Binomial Pricing Model (1) -Two-steps tree

現在我們可以將 One step Tree拓展到 Two steps 的情況。
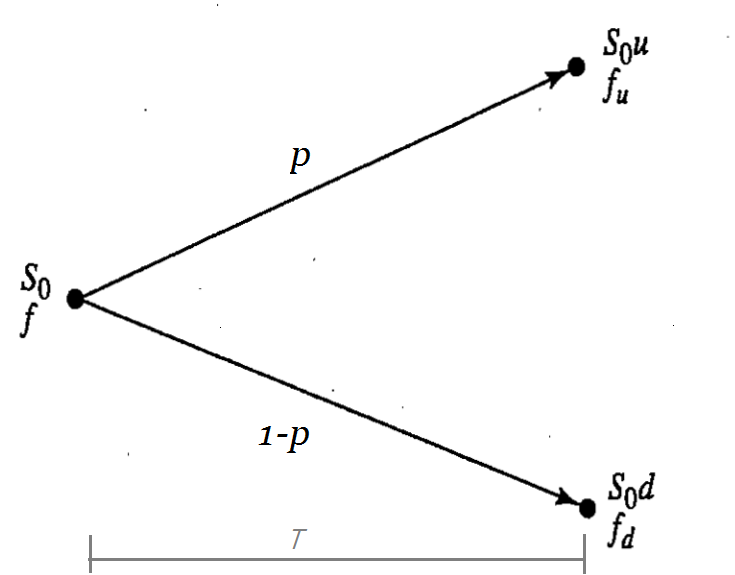
在前篇文章我們有提過，事實上如果把二項樹的step拓展到 無窮大，則Binomial pricing會收斂成為 Black-Scholes formula。

我們手上現在有兩種方法 (此兩種方法等價)來對選擇權進行定價：
1. Binomial Pricing：
2. Risk-Neutral Pricing：風險中性機率 $P$ 再任意二項樹的步都是定值 (因為投資人對風險漠不關心，故股票上漲或下跌對投資人來說沒有影響。故 $P$ 值不變).

先給個例子看看兩步的二項樹是怎麼回事：

Example
現在考慮一個 兩步的二項樹：

今日股價 $S_0 =20$，下圖二項樹的每一步中股價上漲 或者下跌 $10 \%$，假設二項樹中每一步長度$h$為3個月 $h=3/12$ (亦即兩步為 6個月 $T=6/12$)，無風險利率 $r =12 \%$ p. a. (連續複利)，考慮 執行價格為 $K=21$ 的 歐式 看漲選擇權 ( European Call option) 。

我們這邊使用 風險中性定價法求解 $f$：關於風險中性定價有興趣的讀者請參考
[衍生商品] 風險中性定價 (Risk-Neutral Pricing)

步驟如下：

1. 首先求解 (二項樹中 任意一步的) 風險中性機率 $P$：
其中 $r =0.12, h=3/12, u=1.1, d=0.9$，可解得
 \[
P = \frac{{{e^{r h}} - d}}{{u - d}} =0.6523
\]
2. 接著我們可以計算各節點的 看漲選擇權 價格：
首先計算 到期時 at expiration $T$ (6個月) 的 看漲選擇權 價格
\[\left\{ \begin{array}{l}
{f_{uu}} = \max \{ {S_T} - K,0\}  = \max \{ 24.2 - 21,0\}  = 3.2\\
{f_{ud}} = \max \{ {S_T} - K,0\}  = \max \{ 19.8 - 21,0\}  = 0\\
{f_{dd}} = \max \{ {S_T} - K,0\}  = \max \{ 16.2 - 21,0\}  = 0
\end{array} \right.
\]接著再計算中間節點的 看漲選擇權價格 (3個月 $h=3/12$)
\[\left\{ \begin{array}{l}
{f_u} = \left( {P{f_{uu}} + \left( {1 - P} \right){f_{du}}} \right){e^{ - rh}} = \left( {0.6523\left( {3.2} \right) + 0} \right){e^{ - 12\% \left( {3/12} \right)}} = 2.0257\\
{f_d} = \left( {P{f_{du}} + \left( {1 - P} \right){f_{dd}}} \right){e^{ - rh}} = \left( {0 + 0} \right){e^{ - 12\% \left( {3/12} \right)}} = 0
\end{array} \right.
\]最後在計算 $f$
\[f = \left( {P{f_u} + \left( {1 - P} \right){f_d}} \right){e^{ - rh}} = \left( {0.6523\left( {2.0257} \right) + 0} \right){e^{ - 12\% \left( {3/12} \right)}} = 1.2823
\] $\square$

============
那麼現在產生一個簡單的問題，如果是上述例子變成 美式選擇權(American option) 我們可以進行估價嗎?

答案是肯定的。

那麼該怎麼做呢?
Idea: 美式選擇權與歐式選擇權最大差別在於美式選擇權可以在到期時間之前都可以被執行。故我們首先計算歐式選擇權的價格，再逐點討論是否要提早執行該選擇權。

現在回頭再看看剛剛我們解完的 歐式看漲選擇權 的例子：

現在我們逐點討論是否要提早執行該選擇權。

NOTE:
在解題之前我們先注意到一個common sense：
美式 看漲選擇權 在股票未配發股息 的情況之下，永遠都不應該提早執行 (WHY!?)，

因為如果立刻執行我們會得到 $S - K$，但是如果我們不選擇立刻執行而是把美式選擇權賣出，由於美式選擇權可以在到期之前隨時執行，故其價格會比歐式選擇權 要來的高，則我們會得到選擇權價格有如下關係：
\[
C_{american} \geq C_{european}
\]又由歐式看漲選擇權我們知道選擇權的價格具有下界 (內部價值 + 時間價值 $ max\{ S-K, 0\}$)：故我們知道歐式選擇權會有如下關係
 \[ C_{european} \geq S-K
\]，故合併上式我們得到
\[
C_{american} \geq C_{european} \geq S-K
\]這說明了如果立刻執行只有得到下界 $S-K$，但我們如果賣出 美式看漲選擇權則可以得到 $C_{american}$，這說明了 看漲選擇權在未配發股息的情況永遠不該提早執行。以下分析可以作為一個驗證：


現在我們開始逐點討論，對上述例子而言，是否要提早執行 美式選擇權

注意到如果我們考慮 到期時 at expiration $T$，則我們的美式選擇權 $f_{uu}, f_{du}, f_{dd}$ 三點與歐式選擇權價格相同 (因為已經到期!)。

故我們只需討論 $f_u, f_d$ 以及 $f$ 是否需要提早執行。

首先檢驗 $f_u$ (亦即股票從 $20$ 上漲到 $22$的情況)，歐式選擇權計算的結果是 $f_u = 2.0257$，
現在如果是美式選擇權，且如果我們在此時 執行選擇權會得到 $\max\{S_{h=3month} - K, 0 \} = \max\{22 - 21, 0 \} =1$，可以發現 $f_u =2.0275 >1 $ 故不執行。

接著檢驗 $f_d$ (亦即股票從 $20$ 下跌到 $18$的情況)，歐式選擇權計算的結果是 $f_u = 0$，
現在如果是美式選擇權，且如果我們在此時 執行選擇權會得到 $\max\{S_{h=3month} - K \} = \max\{18 - 21, 0 \} =0$，可以發現 $f_u =0 = 0 $ 故不執行。

最後再檢驗 $f$ (亦即現在 )，歐式選擇權計算的結果是 $f = 1.2823$，
現在如果是美式選擇權，且如果我們在此時 執行選擇權會得到 $\max\{S_{h=0} - K \} = \max\{20 - 21, 0 \} =0$，可以發現 $f_u =0 = 0 $ 故不執行。

=====================

現在我們來看個 美式看跌選擇權的例子

Example
同上例，考慮一個 兩步的二項樹：

今日股價 $S_0 =20$，下圖二項樹的每一步中股價上漲 或者下跌 $10 \%$，假設二項樹中每一步長度$h$為3個月 $h=3/12$ (亦即兩步為 6個月 $T=6/12$)，無風險利率 $r =12 \%$ p. a. (連續複利)，考慮 執行價格為 $K=21$ 的 美式 看跌選擇權 ( American Put option) 。

我們這邊使用 風險中性定價法求解 $f$：同樣的第一步先求解 歐式看跌選擇權在做逐步討論

步驟如下：

1. 首先求解 (二項樹中 任意一步的) 風險中性機率 $P$：
其中 $r =0.12, h=3/12, u=1.1, d=0.9$，可解得
 \[
P = \frac{{{e^{r h}} - d}}{{u - d}} =0.6523
\]
2. 接著我們可以計算各節點的 看跌選擇權 價格：
首先計算 到期時 at expiration $T$ (6個月) 的 看跌選擇權 價格
\[\left\{ \begin{array}{l}
{f_{uu}} = \max \{  K - S_T,0\}  = \max \{ 21-24.2 ,0\}  = 0\\
{f_{ud}} = \max \{  K - S_,0\}  = \max \{21 - 19.8,0\}  = 1.2\\
{f_{dd}} = \max \{  K - S_,0\}  = \max \{ 21-16.2,0\}  = 4.8
\end{array} \right.
\]接著再計算中間節點的 看跌選擇權價格 (3個月 $h=3/12$)
\[\left\{ \begin{array}{l}
{f_u} = \left( {P{f_{uu}} + \left( {1 - P} \right){f_{du}}} \right){e^{ - rh}} = 0.4049\\
{f_d} = \left( {P{f_{du}} + \left( {1 - P} \right){f_{dd}}} \right){e^{ - rh}} = 2.3793
\end{array} \right.
\]最後在計算 $f$
\[f = \left( {P{f_u} + \left( {1 - P} \right){f_d}} \right){e^{ - rh}}  = 1.0591 \ \ \ \ \square
\]
故我們可得到如下 兩步的 二項樹圖：

現在我們逐點討論美式選擇權是否要提早執行。

同樣地，注意到如果我們考慮 到期時 at expiration $T$，則我們的美式 看跌選擇權 $f_{uu}, f_{du}, f_{dd}$ 三點與歐式 看跌選擇權價格相同 (因為已經到期!)。

故我們只需討論 $f_u, f_d$ 以及 $f$ 是否需要提早執行。

首先檢驗 $f_u$ (亦即股票從 $20$ 上漲到 $22$的情況是否需要提早執行)，歐式 看跌 選擇權計算的結果是 $f_u = 0.4049$，
現在如果是美式 看跌選擇權，且如果我們在此時 執行選擇權會得到 $\max\{K-S_{h=3month} , 0 \} = \max\{21-22, 0 \} = 0$，(out of money!) ，故不執行。

接著檢驗 $f_d$ (亦即股票從 $20$ 下跌到 $18$的情況是否需要提早執行)，歐式 看跌選擇權計算的結果是 $f_u = 0$，
現在如果是美式看跌選擇權，且如果我們在此時 執行選擇權會得到 $\max\{ K-S_{h=3month} \} = \max\{21-18, 0 \} =3$，可以發現 $f_u =2.3793 < 3 $ 故此時提早執行有利投資人!!。故對美式 看跌選擇權而言， $f_d =2.3793 $需被 $f_{d_{american}} = 3$ 替換!

且因為 $f_d$ 已經被 $f_{d_{american}}$取代，故我們需要重新計算 $f$
\[
f = f_{american} = \left( {P{f_u} + \left( {1 - P} \right){f_{d_{american}}}} \right){e^{ - rh}}=1.2686
\]
最後再檢驗我們剛計算出來的 新 $f$ (亦即現在 是否需要提早執行 )，歐式 看跌選擇權計算的結果是 $f = 1.2686$，
現在如果是美式 看跌選擇權，且如果我們在此時 執行選擇權會得到 $\max\{ K - S_{h=0} \} = \max\{21-20, 0 \} =1$，可以發現 $f_u =1.2686 >1 $ 故不執行。

故美式 看跌選擇權 的價格 $f_{american} = 1.2685$
歐式 看跌選擇權最 的價格 $f = 1.0591$


ref: John C. Hull, Options, Futures and Other Derivatives 7th.

[衍生商品] 風險中性定價 (Risk-Neutral Pricing)

現在介紹另外一種定價選擇權的方式。
稱作 風險中性定價 (Risk-Neutral Pricing)。

簡單說就是我們假設一個新世界，在這個世界中的投資人都為風險中性。

這是甚麼意思呢?

真實世界中，投資人大多為風險趨避者 (Risk-Averse)；亦即投資人不喜歡風險。如果一旦有風險產生，投資人會要求額外的報酬當作補償 (風險溢價 Risk premium)；但風險中性世界的假設是投資人對風險都持中性態度，亦即對風險並不關心。也就是說 若我們處在一個世界是投資者 對風險 不要求 任何額外的補償。則稱此世界為 風險中性 (Risk-Neutral) 世界

則我們可以定義 風險中性機率 $P$ 為風險中性世界中股價上漲的機率

現在考慮下面二項樹

上圖表示在 今日股價為 $S_0$ ，並且考慮在到期時間 $T$ 時，有機率 $P$ 預期股價會上漲成 $S_0 \cdot u$；或者有機率 $(1-P)$ 預期股價會下跌成 $S_0 \cdot d$

NOTE: 注意到上述的 $P$ 為前述定義的風險中性機率。

那麼對於 在到期時間 $T$ 時候的預期股價 $E\left[ {{S_T}} \right] $ 可以寫做：
\[E\left[ {{S_T}} \right] = {S_0}{e^{rT}} = P \cdot \left( {{S_0}u} \right) + (1 - P) \cdot {S_0}d
\]那麼我們可以把 今日股價 $S_0$ 寫成 對到期時間$T$時候，預期股價收益的折現：
\[
{S_0} = \left( {P \cdot \left( {{S_0}u} \right) + (1 - P) \cdot {S_0}d} \right){e^{ - rT}}
\] 由上式我們可以推得 風險中性機率 $P$ 如下：
\[
\Rightarrow P = \frac{{{e^{rT}} - d}}{{u - d}}
\]同樣的，我們也可以透過折現計算 今日 預期選擇權的價格 為 預期收益的折現：
\[
f = \left( {P \cdot {f_u} + (1 - P) \cdot {f_d}} \right){e^{ - rT}} \ \ \ \ (*)
\]

Comment:
1. 風險中性定價方法在計算選擇權價格 較 二項樹求解法容易 (但兩者等價)。因為我們只需先解得 風險中性機率 $P$ 再帶入 $(*)$ 即可求解 $f$。

2. 風險中性機率 $P$ 與真實世界中 股票上漲的機率並不相同!



現在我們考慮一個新的問題：

如果考慮 配發股息情況該如何修正風險中性機率??

考慮與上圖相同的一步 二項樹模型：

其中 $S_0$ 為當前股價，$u$ 為上升因子， $d$ 為下降因子，$f_u$ 為如果股價上升到 $S_u$ 所對應的選擇權價格，$f_d$ 為如果股價下跌到 $S_d$ 所對應的選擇權價格，且給定 $r$ 無風險年利率以連續複利計，$T$ 為到期時間 (以年計算)。則原本不考慮配發股息的風險中性機率 ( Risk-Neutral Probability) $P$ 為
\[
S_0 = (S_0 u P + S_0 d (1-P)) e^{-rT}
\]故整理上式，可得 Risk-Neutral Probability $P$ 為
\[P = \frac{{{e^{rT}} - d}}{{u - d}}
\]
但是現在如果我們考慮標的股票有配發股息的情況，且股息配發為連續複利 $q$ (continuous dividend yield)，則原本的 Risk-Neutral Probability 需進行修正：
\[
S_0 e^{-qT}= (S_0 u P + S_0 d (1-P)) e^{-rT}
\]故 考慮配發連續複利股息的  Risk-Neutral Probability 為
\[P = \frac{{{e^{\left( {r - q} \right)T}} - d}}{{u - d}}\]


注意到上述的 Risk-Neutral Probability 求解 option price 的方法跟之前我們介紹的 Binomial Pricing Method 求出的 Option Price 等價，我們現在看個例子來展示此想法：

Example (Equivalent Pricing Approach)
考慮當前股價 $40$，且已知三個月後股價要麼為 $45$ 或者 $35$，且無風險年利率為 $8%$ 以每三個月複利計算，現在是計算 三個月到期且執行價格為 $40$ 的 European Put Option 的合理價格。並且驗證 Risk-Neutral pricing 與 No-arbitrage argument 答案相等。

Solution
首先改寫已知資訊：
\[
S_0 =40, S_0 u=45, S_0 d=35, r_m:=r_{\text{quarterly}}= 0.08, K=40, T=3/12
\] 我們可繪製如前所敘的 Binomial Tree

注意到此題的利率為 每三個月複利計算，故我們需先將此無風險改為連續複利 $r_c$的形式利用轉換式： (有興趣的讀者請參考 [投資理論] Interest Rates and Continuous Compounding.)
\[
{\left( {1 + \frac{{{r_m}}}{m}} \right)^m} = {e^{{r_c}}}
\] 其中 $m$ 為每年複利計算次數，由題目可知為每三個月計算一次，故一年計算複利 4次；亦即 $m=4$，將此參數帶入上述轉換利率式可得連續複利的無風險利率 $r_c$
\[\begin{array}{l}
{\left( {1 + \frac{{0.08}}{4}} \right)^4} = {e^{{r_c}}}\\
 \Rightarrow {r_c} = 0.0792
\end{array}
\] 有了 $r_c$ 我們可開始計算 Risk-Neutral Probability
\[\begin{array}{l}
{S_0} = ({S_0}uP + {S_0}d(1 - P)){e^{ - {r_c}T}}\\
 \Rightarrow 40 = (45P + 35(1 - P)){e^{ - 0.0792 \times \frac{3}{{12}}}}\\
 \Rightarrow P = 0.58
\end{array}
\] 再者由於此為 Put option，故
\[\left\{ \begin{array}{l}
{f_u} = \max \left\{ {K - {S_0}u,0} \right\} = \max \left\{ {40 - 45,0} \right\} = 0\\
{f_d} = \max \left\{ {K - {S_0}d,0} \right\} = \max \left\{ {40 - 35,0} \right\} = 5
\end{array} \right.
\]現在我們可以計算選擇權價格 $f$：
\[\begin{array}{l}
f = \left[ {{f_u}P + {f_d}\left( {1 - P} \right)} \right]{e^{ - rT}}\\
 \Rightarrow f = \left[ {0 \times 0.58 + 5 \times \left( {1 - 0.58} \right)} \right]{e^{ - 0.0792 \times \frac{3}{{12}}}}\\
 \Rightarrow f = 2.0588
\end{array}\]

現在我們利用 Binomial No-Arbitrage Method：
建構一無風險投資組合：

買入 $\Delta$ 股股票
借入 $B$ 元 債卷

且上述的無風險投資組合必須複製選擇權的payoff，則我們可得
\[\begin{array}{l}
\left\{ \begin{array}{l}
{S_0}u\Delta  + B{e^{rT}} = {f_u}\\
{S_0}d\Delta  + B{e^{rT}} = {f_d}
\end{array} \right. \Rightarrow \left\{ \begin{array}{l}
45\Delta  + B{e^{0.0792 \times \frac{3}{{12}}}} = 0\\
35\Delta  + B{e^{0.0792 \times \frac{3}{{12}}}} = 5
\end{array} \right.\\
 \Rightarrow \left\{ \begin{array}{l}
\Delta  =  - 0.5\\
B = 22.0589
\end{array} \right.
\end{array}\]
故可知需要 賣出 $\Delta = 0.5$ 股票，且借入 $B=22.0589$ 元，且 put option 的價格為
\[
f = S_0 \Delta + B = 40 (-0.5) + 22.0589 =2.0589
\] 上述答案與我們使用 Risk-Neutral Probability 所求的答案相等。 $\square$


ref: John C. Hull, Options, Futures and Other Derivatives 7th.

[衍生商品] 淺談 Binomial Pricing Model (0) - One-step tree case

一般而言 選擇權(Option)的定價模型 大致上有兩種方法：
一種為 二項樹定價法 (Binomial Pricing)  另一種為 Black-Scholes Model (for continuous time)。

NOTE:
1. 事實上 Binomial pricing 取極限會得到Black-Scholes Model)
2. 二項樹定價法有另一個等價的方法求解較為簡便，叫做risk-netural pricng method，關於 risk-netural pricing model 有興趣的讀者可參閱BLOG相關文章: [衍生商品] 風險中性定價 (Risk-Neutral Pricing): 本文在此不討論此法。

這次要介紹的是 Binomial Pricing Method：來幫助我們找出合理的選擇權價格。
基本想法如下：
考慮市場為無套利機會(No-Arbitrage opportunity )的市場，則我們可以建構一組能產生與 選擇權相同的 payoff 的投資組合 。因為既然 payoff 相同則其價值必須相同( 由無套利機會假設兩者等價)。故此我們便可計算選擇權的(合理)價格。

以下為一個簡單的例子說明這個想法

Example
考慮 現時股價 $S_0 = \$ 20$，且已知三個月後股價要麼為 $S_u = \$ 22$ 或者 $ S_d = \$ 18$ (只有此兩種可能)，另外考慮 無風險利率為 $r=12\%$ p.a. (採連續複利)，

現在我們想估計
3個月後到期 ($T=3/12$)、 執行價格(Strike price) $K= \$21$ 的 看漲選擇權 (Call option) 價格應該是多少?

則我們可建構如下二項樹 (點圖放大)：

上圖可以發現如果三個月後的股價為 $22$，看漲選擇權的payoff為 $\max\{S_T - K, 0 \} = \max\{22-21,0 \}=1 $；
反之如果三個月後的股價為 $18$ ，則看漲選擇權對應的payoff為 $\max\{S_T - K, 0 \} = \max\{18-21,0 \}=0 $

那麼現在想要回推 "今日" 看漲選擇權的合理價格應該是多少?

由之前的想法，我們可以建立一個投資組合來 "模仿" or "複製" 看漲選擇權 的收益行為：
故考慮如下投資組合
----------------------------
假設在"今日" 我們
買入 " $ +\Delta$ 股"  股票
投資 " $ +B$ 元 " 債卷 (此債卷提供投資者 無風險利率 $r$)
----------------------------

則三個月後此投資組合的市值，由無套利機會假設可知，必須與選擇權產生的收益相同。故我們得到下圖 (點圖放大)

故我們得到
\[\left\{ {\begin{array}{*{20}{l}}
{22\Delta  + B{e^{12\%  \cdot \left( {3/12} \right)}} = 1}\\
{18\Delta  + B{e^{12\%  \cdot \left( {3/12} \right)}} = 0}
\end{array}} \right.\]上式可求解 $\Delta$ 與 $B$：
\[
\left\{ \begin{array}{l}
\Delta  = 0.25\\
B =  - 4.3670
\end{array} \right.
\] 注意到 $B$ 為負值，亦即我們原本假設為 要投資 $B$ 元 到無風險利率的債卷，但事實上是要 "借入" $4.367$ 元。

那麼有了 $\Delta$ 與 $B$ 便可以回答到底 今日 看漲選擇權的合理價格是多少？ 我們說此價格必須等同於我們所建構的投資組合：亦即買入 0.25股 股價為 $20$ 的股票 再借入 $4.367$元，亦即
\[
20 \Delta + B = 20 \cdot (0.25) - 4.367 = 0.633
\] 此即為我們 看漲選擇權的 (今日購入) 合理價格。 $\square$

Comment:
1. 上述唯一的假設是市場為 無套利機會 。注意到我們並不須知道股票上漲的機率是多少。

2. 如果 賣出一份看漲選擇權 (Short a call) + 購入 0.25股的股票 (Long 0.25 $\Delta$ share) 所建構而成的投資組合會發生甚麼情況?

如果我們在今日用 $0.633$ 賣出看漲選擇權，

現在考慮當三個月後股票價格上漲到 $22$ 時：
看漲選擇權會被執行 (因為 in the money, $22 > 21 = K$)，故要付1元出去，但我們因為在今日買入 $0.25$ 股 股票，故三個月後此 Short a call + Long $0.25 \Delta$  share 的組合價值為$0.25 \cdot 22 -1 = 4.5$

如果考慮當三個月後股票價格下跌到 $18$時：
則看漲選擇權 不會被執行 (因為 out of money, $18 < K=21$)，故我們三個月後 Short a call + Long $0.25 \Delta$  share 的組合價值為
$0.25 \cdot 18 +0 = 4.5$

會發現不論股票上漲或下跌，我們的組合價值都固定為 $4.5$。故此組合為無風險組合(riskless portfolio)。

=============

Generalization of the example

現在我們可以將上述的例子推廣到一般的情況：

現在考慮 當前股價 $S_0$ ，且 當前 選擇權 (可為call option / put option)價格為 $f$  (我們要求解此 $f=?$)， 假定選擇權的到期時間為 $T$ ，在期限內股票價格會由 $S_0$ 上漲到 $S_0 \cdot u$ 或者由 $S_0$ 下降到 $S_0 \cdot d$，其中 $u >1, d<1$；且對應的上漲選擇權價格為 $f_u$，下跌選擇權價格為 $f_d$，則我們可以繪製如下二項樹圖：

那麼我們該如何求解 $f$ ??

由前述例子可知我們要建構一個投資組合使其到期的payoff 等同於 對應的選擇權價格 ($\Rightarrow$ 今日 payoff 也必須相等)。故如前例所示，我們建立投資組合如下：
----------------------------
假設在"今日" 我們
買入 " $ +\Delta$ 股"  股票
投資 " $ +B$ 元 " 債卷 (此債卷提供投資者 無風險利率 $r$)
----------------------------

則我們可寫出
\[\left\{ {\begin{array}{*{20}{l}}
{{S_0}u\Delta  + B{e^{rT}} = {f_u}}\\
{{S_0}d\Delta  + B{e^{rT}} = {f_d}}
\end{array}} \right. \Rightarrow \left\{ {\begin{array}{*{20}{l}}
{\Delta  = \frac{{{f_u} - {f_d}}}{{{S_0}\left( {u - d} \right)}}}\\
{B = {e^{ - rT}}\left( {\frac{{u{f_d} - d{f_u}}}{{u - d}}} \right)}
\end{array}} \right.
\]故今日合理的選擇權價格
\[\begin{array}{l}
f = \Delta {S_0} + B\\
 \Rightarrow f = \frac{{{f_u} - {f_d}}}{{{S_0}\left( {u - d} \right)}}{S_0} + {e^{ - rT}}\left( {\frac{{u{f_d} - d{f_u}}}{{u - d}}} \right)
\end{array}\]

Comment:
1.  ${\Delta  = \frac{{{f_u} - {f_d}}}{{{S_0}u - {S_0}d}}}$ 代表 選擇權 與 股票價格 之間的變化率 (斜率)，
對於 Call option 而言，$0 \leq \Delta_{call} \leq 1$；(當股價上升的時候投資人獲利。)
對於 Put Option而言， $-1 \leq \Delta_{put} \leq 0$。(當股價下跌的時候投資人獲利。)
另外若考慮為連續時間的情況 $\Delta := \frac{{\partial C}}{{\partial S}}$

2. 觀察 前述選擇權定價的式子
\[{f = \frac{{{f_u} - {f_d}}}{{{S_0}\left( {u - d} \right)}}{S_0} + {e^{ - rT}}\left( {\frac{{u{f_d} - d{f_u}}}{{u - d}}} \right)}
\] 我們可發現 定價選擇權需要的資訊為
1. 現時股價 $S_0$
2. 執行價格 $K$ (計算 $f_u, f_d$)
3. 無風險利率 $r$
4. 到期時間 $T$
5. $u$ & $d$ <~ 上升因子/與下降因子乘數；此兩者會與 volatility 有關。會在之後再行介紹。


延伸閱讀
[衍生商品] 淺談 Binomial Pricing Model (1) -Two-steps tree

ref: John C. Hull, Options, Futures and Other Derivatives 7th.